Hi all. Now my supervisor and I are preparing a monograph for publication, where we are trying to in simple terms talk about the basics digital processing images. This article reveals a very simple, but at the same time very effective technique for improving image quality - histogram equalization.
For simplicity, let's start with monochrome images (i.e., images containing information only about the brightness, but not about the color of the pixels). An image histogram is a discrete function H defined on the set of values , where bpp is the number of bits allocated to encode the brightness of one pixel. Although not required, histograms are often normalized to the range by dividing each value of the H[i] function by the total number of pixels in the image. In Table. 1 shows examples of test images and histograms built on their basis:
Tab. 1. Images and their histograms
Having carefully studied the corresponding histogram, we can draw some conclusions about the original image itself. For example, histograms of very dark images are characterized by the fact that non-zero values of the histogram are concentrated near zero brightness levels, and vice versa for very light images - all non-zero values are concentrated on the right side of the histogram.
Intuitively, we can conclude that the most convenient image for human perception will be an image whose histogram is close to a uniform distribution. Those. for improvement visual quality it is necessary to apply such a transformation to the image so that the histogram of the result contains all possible brightness values and, at the same time, in approximately the same amount. This transformation is called histogram equalization and can be done using the code in Listing 1.
Listing 1. Implementing a histogram equalization procedure
- procedure TCGrayscaleImage. Histogram Equalization ;
- const
- k = 255
- h: array [ 0 .. k ] of double ;
- i, j: word;
- begin
- for i := 0 to k do
- h[i] := 0 ;
- h[ round (k * self . Pixels [ i, j] ) ] : = h[ round (k * self . Pixels [ i, j] ) ] + 1 ;
- for i := 0 to k do
- h[ i] : = h[ i] / (self . Height * self . Width ) ;
- for i := 1 to k do
- h[ i] : = h[ i - 1 ] + h[ i] ;
- for i := 0 to self . Height - 1 do
- for j := 0 to self . Width - 1 do
- self . Pixels [ i, j] : = h[ round (k * self . Pixels [ i, j] ) ] ;
- end ;
As a result of equalizing the histogram, in most cases the dynamic range of the image is significantly expanded, which makes it possible to display previously unnoticed details. This effect is especially pronounced on dark images, which is shown in Table. 2. In addition, it is worth noting one more important feature of the equalization procedure: unlike most filters and gradation transformations that require setting parameters (aperture and gradation transformation constants), histogram equalization can be performed in a fully automatic mode without operator participation.
Tab. 2. Images and their histograms after equalization

You can easily see that the histograms after equalization have a kind of noticeable discontinuities. This is due to the fact that the dynamic range of the output image is wider than that of the original image. Obviously, in this case, the mapping considered in Listing 1 cannot provide non-zero values in all histogram bins. If you still need to achieve a more natural appearance of the output histogram, you can use a random distribution of the values of the i-th histogram bin in some of its neighborhood.
Obviously, histogram equalization makes it easy to improve the quality of monochrome images. Naturally, I would like to apply a similar mechanism to color images.
Most not very experienced developers present an image in three RGB color channels and try to apply the histogram equalization procedure to each color individually. In some rare cases, this allows you to succeed, but in most cases the result is so-so (colors are unnatural and cold). This is because the RGB model does not accurately represent human color perception.
Let's think about another color space - HSI. This color model (and others related to it) is very widely used by illustrators and designers, as it allows you to operate with more familiar concepts of hue, saturation and intensity.
If we consider the projection of the RGB cube in the direction of the white-black diagonal, then we get a hexagon, the corners of which correspond to the primary and secondary colors, and all gray shades (lying on the diagonal of the cube) are projected to the central point of the hexagon (see Fig. 1):

Rice. 1. Color cube projection
In order to be able to encode all the colors available in the RGB model using this model, you need to add a vertical lightness (or intensity) axis (I). The result is a hexagonal cone (Fig. 2, Fig. 3):

Rice. 2. Pyramid HSI (tops)
In this model, hue (H) is given by the angle relative to the red axis, saturation (S) characterizes the purity of the color (1 means a completely pure color, and 0 corresponds to a shade of gray). At a saturation value of zero, the hue has no meaning and is undefined.

Rice. 3. Pyramid HSI
In Table. Figure 3 shows the decomposition of the image into HSI components (white pixels in the tone channel correspond to zero saturation):
Tab. 3. color space HSI

It is believed that to improve the quality of color images, it is most effective to apply the equalization procedure to the intensity channel. This is exactly what is shown in Table. four
Tab. 4. Equalization of various color channels

I hope you found this material at least interesting, at most useful. Thank you.
There are three main methods for increasing the contrast of an image:
- linear histogram stretching (linear contrasting),
- histogram normalization,
- alignment (linearization or equalization, equalization) of the histogram.
Linear stretch comes down to assigning new intensity values to each pixel in the image. If the intensities of the original image changed in the range from to , then it is necessary to linearly "stretch" the indicated range so that the values change from 0 to 255. To do this, it is enough to recalculate the old intensity values for all pixels according to the formula , where the coefficients are simply calculated based on the fact that that the border should go to 0, and - to 255.
Histogram normalization unlike the previous method, it does not stretch the entire range of intensity changes, but only its most informative part. The informative part is a set of histogram peaks, i.e. intensities that occur more often than others in the image. Bins corresponding to rare intensities are discarded during normalization, then the usual linear stretching of the resulting histogram is performed.
alignment histogram is one of the most common ways. The purpose of equalization is that all brightness levels would have the same frequency, and the histogram would correspond to a uniform distribution law. Let's say we're given a grayscale image that has pixel resolution. The number of pixel brightness quantization levels (number of bins) is . Then, on average, for each brightness level should fall ![]() pixels. The underlying math lies in matching the two distributions. Let be random variables describing the change in the intensity of pixels in images, be the intensity distribution density on the original image, and be the desired distribution density. It is necessary to find a transformation of distribution densities , which would allow obtaining the desired density:
pixels. The underlying math lies in matching the two distributions. Let be random variables describing the change in the intensity of pixels in images, be the intensity distribution density on the original image, and be the desired distribution density. It is necessary to find a transformation of distribution densities , which would allow obtaining the desired density:

Denote by and integral laws of distribution of random variables and . From the condition of probabilistic equivalence it follows that ![]() . We write the integral distribution law by definition:
. We write the integral distribution law by definition:
Hence we get that
It remains to find out how to estimate the integral distribution law . To do this, you must first build a histogram of the original image, then normalize the resulting histogram by dividing the value of each bin by the total number of pixels . The bin values can be thought of as an approximation of the distribution density function. Thus, the value of the integral distribution function can be represented as a sum of the following form:

The constructed estimate can be used to calculate new intensity values. Note that the above histogram transformations can be applied not only to the entire image, but also to its individual parts.
The OpenCV library implements the equalizeHist function, which provides image contrast enhancement through histogram equalization [ , ]. The function prototype is shown below.
void equalizeHist(const Mat& src, Mat& dst)
The function works in four steps:
The following is an example of a program that provides histogram equalization. The application takes as an argument command line the name of the original image. After performing the histogram equalization operation, display the original image 1 The image used is part of the PASACL VOC 2007 base., converted to grayscale (Fig. 7.11, left), and an image with a histogram equalized (Fig. 7.11, right).
#include \n\ \t
- image file name\n"; int main(int argc, char* argv) ( const char *initialWinName = "Initial Image", *equalizedWinName = "Equalized Image"; Mat img, grayImg, equalizedImg; if (argc< 2)
{
printf("%s", helper);
return 1;
}
// загрузка изображения
img = imread(argv, 1);
// преобразование в оттенки серого
cvtColor(img, grayImg, CV_RGB2GRAY);
// выравнивание гистограммы
equalizeHist(grayImg, equalizedImg);
// отображение исходного изображения и гистограмм
namedWindow(initialWinName, CV_WINDOW_AUTOSIZE);
namedWindow(equalizedWinName, CV_WINDOW_AUTOSIZE);
imshow(initialWinName, grayImg);
imshow(equalizedWinName, equalizedImg);
waitKey();
// закрытие окон
destroyAllWindows();
// осовобождение памяти
img.release();
grayImg.release();
equalizedImg.release();
return 0;
}

Rice. 7.11.
With all element-by-element transformations, the probability distribution law that describes the image changes. With linear contrasting, the form of the probability density is preserved, however, in the general case, i.e. with arbitrary values of the linear transformation parameters, the parameters of the probability density of the transformed image change.
Determining the probabilistic characteristics of images that have undergone nonlinear processing is a direct task of analysis. When solving practical problems of image processing, an inverse problem can be posed: according to the known form of the probability density p f(f) and the desired form p g(g) define the desired transformation g= ϕ( f) to which the original image should be subjected. In the practice of digital image processing, transforming an image to an equiprobable distribution often leads to a useful result. In this case
where g min and g max - minimum and maximum brightness values of the converted image. Let us determine the characteristic of the converter that decides this task. Let f and g bound by function g(n, m) = j( f(n, m)), a Pf(f) and Pg(g) are the integral distribution laws for the input and output brightness. Taking into account (6.1), we find:

Substituting this expression into the probabilistic equivalence condition
![]()
after simple transformations, we obtain the relation
which is a characteristic g(n, m) = j( f(n, m)) in the problem being solved. According to (6.2), the original image undergoes a nonlinear transformation, the characteristic of which is Pf(f) is determined by the integral distribution law of the original image. After that, the result is reduced to the given dynamic range using the linear contrast operation.
Thus, the probability density transformation assumes knowledge of the integral distribution for the original image. As a rule, there is no reliable information about him. Approximation by analytical functions, due to approximation errors, can lead to a significant difference in the results from the required ones. Therefore, in the practice of image processing, the transformation of distributions is performed in two stages.
At the first stage, the histogram of the original image is measured. For a digital image whose gray scale belongs to the integer range, for example, the histogram is a table of 256 numbers. Each of them shows the number of pixels in the image (frame) that have a given brightness. By dividing all the numbers in this table by the total sample size, equal to the number of samples in the image, an estimate of the probability distribution of the brightness of the image is obtained. Denote this estimate q p f(fq), 0 ≤ fq≤ 255. Then the estimate of the integral distribution is obtained by the formula:

At the second stage, the nonlinear transformation itself (6.2) is performed, which provides the necessary properties of the output image. In this case, instead of the unknown true integral distribution, its estimate based on the histogram is used. With this in mind, all methods of element-by-element transformation of images, the purpose of which is to modify the laws of distribution, are called histogram methods. In particular, a transformation where the output image has a uniform distribution is called equalization (alignment) of the histogram.
Note that the histogram transformation procedures can be applied both to the image as a whole and to its individual fragments. The latter can be useful in the processing of non-stationary images, the characteristics of which differ significantly in different areas. In this case best effect can be achieved by applying histogram processing to individual areas - areas of interest. True, this will change the values of the readings and all other areas. Figure 6.1 shows an example of equalization performed in accordance with the described methodology.
A characteristic feature of many images obtained in real imaging systems is a significant specific gravity dark areas and a relatively small number of areas with high brightness.


Figure 6.1 – An example of image histogram equalization: a) the original image and its histogram c); b) the transformed image and its histogram d)
Equalization of the histogram leads to equalization of the integral areas of uniformly distributed brightness ranges. Comparison of the original (Figure 6.1 a) and processed (Figure 6.1 b) images shows that the redistribution of brightness that occurs during processing leads to an improvement in visual perception.
With all element-by-element transformations, the probability distribution law that describes the image changes. Let's consider the mechanism of this change using the example of an arbitrary transformation with a monotonic characteristic described by a function (Fig. 2.8) that has a single-valued inverse function . Assume that the random variable obeys the probability density . Let be an arbitrary small interval of values of the random variable , and be the corresponding interval of the transformed random variable .
If a value falls into the interval, then the value falls into the interval , which means the probabilistic equivalence of these two events. Therefore, taking into account the smallness of both intervals, we can write an approximate equality:
![]() ,
,
where the modules take into account the dependence of the probabilities on the absolute lengths of the intervals (and the independence of the signs of the increments and ). Calculating from here the probability density of the transformed quantity, substituting instead of its expression through the inverse function and performing the passage to the limit at (and, therefore, ), we obtain:
![]() .
(2.4)
.
(2.4)
This expression allows one to calculate the probability density of the transformation product, which, as can be seen from it, does not coincide with the distribution density of the original random variable. It is clear that the transformation performed has a significant effect on the density, since (2.4) includes its inverse function and its derivative.
The relations become somewhat more complicated if the transformation is not described by a one-to-one function. An example of such a more complex characteristic with an ambiguous inverse function is the sawtooth characteristic in Fig. 2.4, k. However, in general, the meaning of probabilistic transformations does not change in this case.
All element-by-element transformations of images considered in this chapter can be considered from the point of view of the change in the probability density described by expression (2.4). Obviously, under none of them, the probability density of the output product will coincide with the probability density of the original image (with the exception, of course, of a trivial transformation). It is easy to see that with linear contrasting, the form of the probability density is preserved, however, in the general case, i.e., for arbitrary values of the linear transformation parameters, the parameters of the probability density of the transformed image change.
Determining the probabilistic characteristics of images that have undergone nonlinear processing is a direct task of analysis. When solving practical problems of image processing, an inverse problem can be posed: by the known form of the probability density and the desired form, determine the required transformation , which should be subjected to the original image. In the practice of digital image processing, transforming an image to an equiprobable distribution often leads to a useful result. In this case
where and are the minimum and maximum brightness values of the converted image. Let us determine the characteristics of the converter that solves this problem. Let and be related by the function (2.2), and and be the integral distribution laws of the input and output quantities. Taking into account (2.5), we find:
 .
.
Substituting this expression into the probabilistic equivalence condition
after simple transformations, we obtain the relation
which is characteristic (2.2) in the problem being solved. According to (2.6), the original image undergoes a nonlinear transformation, the characteristic of which is determined by the integral distribution law of the original image itself. After that, the result is reduced to the specified dynamic range using the linear contrast operation.
Similarly, solutions to other similar problems can be obtained, in which it is required to bring the distribution laws of the image to a given form. A table of such transformations is given in. One of them, the so-called distribution hyperbolization, involves reducing the probability density of the transformed image to a hyperbolic form:
 (2.7)
(2.7)
If we take into account that when light passes through the eye, the input brightness is logarithmized by its retina, then the resulting probability density turns out to be uniform. Thus, the difference from the previous example lies in taking into account the physiological properties of vision. It can be shown that an image with probability density (2.7) is obtained at the output of a nonlinear element with characteristic
also determined by the integral distribution law of the original image.
Thus, the probability density transformation assumes knowledge of the integral distribution for the original image. As a rule, there is no reliable information about him. The use of analytical approximations for the purposes under consideration is also of little use, since their small deviations from the true distributions can lead to a significant difference in the results from the required ones. Therefore, in the practice of image processing, the transformation of distributions is performed in two stages.
At the first stage, the histogram of the original image is measured. For a digital image, whose grayscale, for example, belongs to the integer range 0...255, the histogram is a table of 256 numbers. Each of them shows the number of points in the frame that have a given brightness. By dividing all the numbers in this table by the total sample size equal to the number of image pixels used, an estimate of the image brightness probability distribution is obtained. We denote this estimate ![]() . Then the estimate of the integral distribution is obtained by the formula:
. Then the estimate of the integral distribution is obtained by the formula:
 .
.
At the second stage, the nonlinear transformation (2.2) itself is performed, which provides the necessary properties of the output image. In this case, instead of the unknown true integral distribution, its estimate based on the histogram is used. With this in mind, all methods of element-by-element transformation of images, the purpose of which is to modify the laws of distribution, are called histogram methods. In particular, the transformation in which the output image has a uniform distribution is called equalization (alignment) of the histograms.
Note that the histogram transformation procedures can be applied both to the image as a whole and to its individual fragments. The latter can be useful in the processing of non-stationary images, the content of which differs significantly in its characteristics in different areas. In this case, the best effect can be achieved by applying histogram processing to individual areas.
The use of relations (2.4)-(2.8) , which are valid for images with a continuous distribution of brightness, is not quite correct for digital images. It should be borne in mind that as a result of processing it is not possible to obtain an ideal probability distribution of the output image, so it is useful to control its histogram.
|
|
|
|
a) original image |
b) processing result |
|
Rice. 2.9. Image Equalization Example |
|
Figure 2.9 shows an example of equalization performed in accordance with the described methodology. A characteristic feature of many images obtained in real imaging systems is a significant proportion of dark areas and a relatively small number of areas with high brightness. Equalization is designed to correct the picture by aligning the integral areas of areas with different brightnesses. Comparison of the original (Fig. 2.9.a) and processed (Fig. 2.9.b) images shows that the redistribution of brightness that occurs during processing leads to an improvement in visual perception.
Perform image processing, visualization and analysis
Image Processing Toolbox™ provides a comprehensive set of reference-standard algorithms and workflow applications for image processing, analysis, visualization, and algorithm development. You can perform image segmentation, image enhancement, denoising, geometric transformations, and image registration using deep learning and traditional image processing techniques. Processing toolbox supports 2D, 3D, and arbitrarily large images.
Image Processing Toolbox applications allow you to automate common image processing workflows. You can interactively segment image data, compare image registration methods, and batch process large datasets. Visualization features and applications allow you to explore images, 3D volumes and videos; adjust the contrast; create histograms; and control visible areas (KINGS).
You can speed up algorithms by executing them on multi-core processors and GPUs. Many toolbox functions support C/C++ code generation for computer vision deployment and prototype analysis.
Beginning of work
Learn the Basics of Image Processing Toolbox
Import, export, and convert
Image data import and export, conversion of image types and classes
Display and exploration
Interactive imaging and exploration tools
Geometric transformation and image registration
Scale, rotate, perform others N-D conversions and align images using intensity correlation, feature matching, or control point mapping
Image filtering and enhancement
Contrast adjustment, morphological filtering, deblurring, ROI based processing
Image segmentation and analysis
Area analysis, structure analysis, pixel and image statistics
Deep Learning for Image Processing
Perform image processing tasks, such as removing image noise and generating high-resolution images from low-resolution images, using convolutional neural networks (requires Deep Learning Toolbox™)









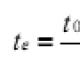


For beginners: breeding a broiler at home Boiled water for broilers
Only lovers will survive
Features of advertising aimed at children
retouching old photos in photoshop retouching old photos
What is an NPO: decoding, definition of goals, types of activities Does a non-profit organization have the right